| АРХИМЕД, ПИФАГОР, ЕВКЛИД, ДЕКАРД, ЛОБАЧЕВСКИЙ... |
Поучительные истории
Записки учителя математики
На своих уроках всегда стараюсь рассказать историю, относящуюся к теме. Что-то мне рассказали в школе, когда я была девочкой, что-то вычитала в разных книжках по истории математики. Пересказываю здесь своими словами, из какой книги что взяла, сказать не берусь.
Начну с закона Архимеда , от которого и возникла идея этой темы.
Архимед был весьма известным и уважаемым ученым у себя в Сиракузах. Однажды царь Сиракуз заподозрил, что золотая корона, которую ему изготовили, на самом деле не полностью золотая. То есть ювелир присвоил себе часть золота, выданного для короны. Царь вызвал Архимеда и поручил ему проверить корону.
Зная плотность золота и тщательно взвесив корону, Архимед рассудил так: если корона золотая, то ее масса будет равна произведению объема на плотность. Если не сойдется, значит, не золотая. Тут-то и возникла проблема: как измерить объем? Форма короны была такой сложной, что никакие измерения не помогали. Долго Архимед ломал над этим голову, пока однажды не полез купаться в слишком наполненную ванну. Вода выплеснулась, а Архимеда осенило: объем вытесненной жидкости равен объему тела, погруженному в эту жидкость! Говорят, он голый бежал по улице с криками "Эврика", что значит "нашел!". Осталось лишь погрузить корону в сосуд с известными размерами, измерить, на сколько повысился уровень воды, и вычислить объем.
Стих на эту тему:
Всяко тело, вперто в воду,
Выпирает на свободу
С силой выпертой воды
Телом, втиснутым туды.
(Это про то, что выталкивающая, или архимедова, сила, равна силе тяжести, действовавшей на вытесненный телом объём жидкости.)
Про деление на ноль.
Не причиним числу мы боль,
Не будем мы делить на ноль!
Про Евклида.
Он тоже был весьма известным и уважаемым ученым, имел много учеников.
Однажды царь Птолемей пригласил Евклида к себе и сказал, что ему тоже хотелось бы изучить геометрию, но царские обязанности не оставляют времени. Нельзя ли как-нибудь выучить геометрию побыстрее? Евклид ответил: «В геометрии нет царских путей».
По другим источникам, это сказал Менехм Александру Македонскому.
Про Декарта, создателя декартовой системы координат.
Когда ему было 50 лет, он тоже был весьма известным и уважаемым ученым. :)
О нем прослышала шведская королева Кристина, которой было 19 лет. Она приложила много усилий, чтобы заполучить Декарта к себе в качестве учителя. На свою беду, он согласился (хотя и не сразу). Кристина считала, что заниматься надо в 5 утра в неотапливаемой библиотеке. Это подорвало его здоровье, он заболел. Декарту послали королевских врачей, он их выставил – так устал, что рад был умереть. Через год после своего приезда в Швецию он умер.
В связи с этим Декарту приписывают фразу: «Математик должен спать, пока не проснется».
(Эту фразу я детям не рассказываю - они и так вечно опаздывают.)
Про Пифагора и иррациональные числа (это 8 класс).
Пифагор был весьма известным и уважаемым ученым. :))
Известен он был не только как математик, но как философ и как политик (с этим, впрочем, у него не очень заладилось – его изгнали). У него была философская школа. Пифагор и его последователи приписывали числам особые сверхъестественные свойства, понимали, что каждая вещь или явление обладают сущностью (содержанием) и видимостью (формой). Форма постигается органами чувств, а сущность – умом и подчинена логике чисел. Познав мир чисел, познаём и сущность вещей. «Все сущее есть число» - лозунг пифагорейцев.
Предполагают, что от пифагорейцев ведет свое начало термин «математика». Пифагорейцы различали четыре матемы (с греч. «матема» - знание, наука, учение через размышление): учение о числах (арифметику), теорию музыки (гармонию), учение о фигурах и измерениях (геометрию) и астрономию с астрологией.
В связи с обожествлением числа у них вышла серьезная неприятность. Под числами они понимали обыкновенные дроби, т.е., по нашим понятиям, рациональные числа. Про то, что бывают иррациональные числа, они не знали. Поэтому, когда выяснилось, что диагональ квадрата не может быть выражена рациональным числом (она равна корню из двух), у них получилось, что не существует такого числа, которое выражает такую обычную вещь, как диагональ квадрата. Это был крах всей философской теории. Произошел раскол. Часть ученых, и Пифогор с ними, считала, что эту страшную тайну надо скрывать. Другая часть считала, что против фактов не попрешь.
После раскола пифагорейского союза образовалось два главных направления: «акузматики» (от греческого слова «акусма» – «священное изречение» ) – сторонники религиозно-мистического учения Пифагора и «математики» – приверженцы науки. От последних и ведется название «математика».
Легенда гласит, что человек по имени Гипас, раскрывший миру страшную тайну про корень из двух, был проклят Пифагором. И в своем первом же путешествии (а греки путешествовали в основном на кораблях) он утонул во время бури. Так сбылось проклятие.
Когда дети не помнят, чему равна диагональ квадрата, я их стыжу, говорю: «Человек жизнь за это отдал, а вы не помните!»
Про алгебру.
Ал-Хорезми – весьма известный... ну, вы понимаете, арабский математик. Написал книгу, навание которой звучит примерно «Китаб аль-джебр и ал-мукабала», сокращенно «аль-джебр». Посвящена была способам решения уравнений. Аль-джебр – перенос членов из одной части уравнения в другую. Ал-мукабала – сокращение равных членов в обеих частях. Алгебра - от аль-джебр. Алгоритм – латинизированная форма его имени.
Теорему Виета проходят в 8 классе.
Франсуа Виет был по образованию и специальности юристом, но отличался любовью к точным наукам. В молодости был офицером.
Нидерланды в то время принадлежали католической Испании, в которой безумствовала инквизиция. Для сношений через Францию со своей провинцией испанцы изобрели сложный шифр. Этот шифр использовался и во время войны с Францией. Король Испании Филипп II был уверен, что никто в мире не сможет его прочесть. Но французский король Генрих IV обратился к Виету, который в течение двух недель нашел ключ к шифру. После этого Генрих сделал Виета своим личным советником.
Французы два года пользовались преимуществами, вытекающими из знания планов своих врагов. После целого ряда поражений испанцы догадались, в чем причина их неудач, и обвинили Виета в том, что он связан с дьяволом. Он был заочно приговорен к сожжению. К счастью, его не выдали инквизиции.
Виет первый ввел буквенные обозначения не только для неизвестных, но и для коэффициентов уравнений. Благодаря этому появилась возможность записать выражения для решения уравнений в виде компактных формул.
Теорема Пифагора
В средние века теорему Пифагора называли «ослиный мост".
Из словаря:
Pons asinōrum = Pons asini
«Мост для ослов», «ослиный мост», перен. камень преткновения или средство, помогающее преодолеть трудность, понять что-либо труднодоступное.
Выражение возникло первоначально среди средневековых школяров как название теоремы Пифагора о квадрате гипотенузы (по форме чертежа, напоминавшего мост - ср. «Пифагоровы штаны").
В некоторых списках «Начал» Евклида эта теорема называлась «теоремой нимфы» за сходство чертежа с бабочкой, что по-гречески называлось нимфой. Но словом этим греки называли еще некоторых богинь, а также вообще молодых женщин и невест. При переводе с греческого арабский переводчик, не обратив внимания на чертеж, перевел слово «нимфа» как «невеста», а не «бабочка". Так появилось ласковое название знаменитой теоремы - «теорема невесты».
Карл Гаусс, прозванный впоследствии «королем математиков», с детства проявлял к математике необыкновенные способности. Учитель же его в школе был очень ленив. Он давал детям задание, чтобы делали подольше, а сам дремал. Выполнив, дети клали свои доски на стол учителю. Однажды учитель дал задание сложить все числа от 1 до 100 в расчете, что до конца урока им работы хватит. Не прошло и минуты, как Гаусс положил свою доску на стол учителю. Тот рассердился – никакого покоя! – но ответ был правильный.
Гаусс заметил, что 1+100=2+99=3+98=...50+51. Оставалось только умножить 50 на 101.
Старинная легенда про изобретателя шахмат.
Рассказывают, что властитель той страны, где были изобретены шахматы, был в таком восторге от этой игры, что призвал к себе изобретателя и приказал просить все, что он захочет. Изобретатель ответил: мне много не надо. На первую клетку шахматной доски положите одно зерно пшеницы, на вторую - 2, на третью - 4, затем 8 и т.д. Это зерно я заберу, и мне достаточно. Правитель приказал отсчитать награду, но выяснилось, что такого количества зерна нет не только во дворце, но и во всей стране! Более того, такое количество зерна человечество не произвело за всю свою историю. Говорят, правитель рассердился и приказал отрубить изобретателю голову. Чтобы не зарывался.
Теорема Фалеса
Фалес – древнегреческий ученый, жил в 6 веке до н.э. Уже в 5 в. до н.э. его имя стало нарицательным для мудреца, т.е. он был весьма известным и уважаемым ученым. :)
Вообще, похоже, что это первый ученый, чье имя дошло до нас. Его считают основоположником философии, а значит, и науки вообще. В математике он первый стал использовать логические рассуждения для доказательства теорем. Ему принадлежит доказательство того, что в равнобедренном треугольнике углы при основании равны.
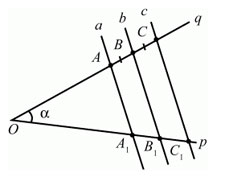 В школе проходят теорему Фалеса, которая гласит: «Если на одной стороне угла поставить точки на равном расстоянии друг от друга и через эти точки провести параллельные прямые, то точки, в которых прямые пересекут другую сторону угла, тоже будут на равном расстоянии друг от друга».
В школе проходят теорему Фалеса, которая гласит: «Если на одной стороне угла поставить точки на равном расстоянии друг от друга и через эти точки провести параллельные прямые, то точки, в которых прямые пересекут другую сторону угла, тоже будут на равном расстоянии друг от друга».
По этому поводу легенда. Фалес приказал рабу завесить окно занавеской, потому что солнце светило слишком ярко и мешало ему сосредоточиться. Занавеска до этого лежала сложенная, и как-то ее повредили, проткнув сразу несколько слоев. Когда раб повесил занавеску на окно, дырки оказались на равном расстоянии друг от друга. Через эти дырки в темной комнтате ворвались лучи света (параллельные), и на полу получились светлые пятнышки – тоже на равном расстоянии! Фалес это заметил, и вместо того, чтобы наказать раба, сформулировал свою теорему.
Как появилась геометрия.
В Древнем Египте вся жизнь протекала на берегах Нила, потому что только там была плодородная почва. Каждый год Нил разливался, нанося на берега толстый слой плодородного ила. Зато он сносил и все заборы и вехи, отделяющие участки друг от друга. Поэтому специальные чиновники приходили и производили раздел заново. Для этого, естественно, надо было производить измерения и построения. Слово «геометрия» переводится как «измерение земли».
Когда в Египет пришли греки, там ничего не изменилось – по-прежнему ходили специально обученные люди с колышками и веревочками. Греки называли их «гарпедонаптами» – натягивателями веревок.
Для построения прямых углов гарпедонапты использовали веревку, завязанную в кольцо.
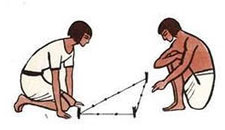 На этой веревке через равные промежутки было завязано 12 узелков. Египтяне знали, что треугольник, у которого одна сторона равна 3, другая 4, а третья 5, является прямоугольным. Они натягивали веревку так, чтобы на одной стороне было три промежутка между узелками, на другой 4, на третьей 5. Примерно как на рисунке.
На этой веревке через равные промежутки было завязано 12 узелков. Египтяне знали, что треугольник, у которого одна сторона равна 3, другая 4, а третья 5, является прямоугольным. Они натягивали веревку так, чтобы на одной стороне было три промежутка между узелками, на другой 4, на третьей 5. Примерно как на рисунке.
И поныне треугольник со сторонами 3, 4, 5 называется египетским.
Никколо Тарталья , итальянский математик 16 века.
В детском возрасте он во время взятия французами Брешии (города, где он родился) получил рану в лицо. В результате у него была плохая дикция, и его прозвали Тарталья – заика. А настоящая фамилия его Фонтана. У его матери не было денег на его обучение, поэтому он даже читать научился сам, не говоря уж о математике.
Тарталья разработал формулу для решения уравнения третьей степени. Эту формулу он показал Джероламо Кардано, а тот опубликовал ее как свою. Возмущенный Тарталья вызвал Кардано на публичный диспут – в те времена это было популярное развлечение. Для спорщиков воздвигались трибуны в большом соборе или на городской площади, собиралась громадная толпа зрителей, с интересом выслушивавшая обе стороны. Надо сказать, что диспуты проводились исключительно на научные темы и при этом были очень популярны.
Тарталья из-за своего физического недостатка проиграл диспут, и формула и поныне называется формулой Кардано.
Про неевклидову геометрию.
Некоторые люди полагают, что суть неевклидовой геометрии в том, что параллельные прямые все-таки пересекаются, а суть теории относительности Эйнштейна в том, что все относительно. То и другое – ерунда.
Насчет теории относительности не возьмусь объяснять, а про неевклидову геометрию возьмусь.
Евклид в своих «Началах», которые служили учебником в течение почти двух тысяч лет, сформулировал 5 аксиом, или постулатов. Пятый из них гласил, что через точку вне прямой может быть проведена лишь одна прямая, параллельная данной. Пафос постулата в том, что прямая лишь одна.
Все эти две тысячи лет математики пытались доказать этот постулат, то есть хотели из аксиомы превратить его в теорему. При этом использовали обычный метод геометрии – доказательство от противного. Предположим, что это не так, тогда... рассуждаем, рассуждаем... приходим к противоречию. Значит, наше предположение неверно, а верно то, что утверждается в теореме.
Если предположить, что 5 постулат неверен, то через точку вне прямой можно провести не одну прямую, параллельную данной. Выводов из этого постулата наделали много, но доказать так и не удавалось. Противоречие не находилось. Вернее, много раз находилось, но каждый раз в доказательствах обнаруживалась ошибка. Так продолжалось до тех пор, пока не появился Николай Иванович Лобачевский.
Лобачевский был одним из трех сыновей бедной вдовы, жили они буквально в нищете, учились в гимназии за казенный счет. Затем он поступил в Казанский университет и уже на первом курсе опубликовал свою первую работу по математике, которая не была оценена, т.к. никто не понял, что там написано. Впоследствии Лобачевский, поработав преподавателем, понял, что не все так сообразительны, как он сам. :) Но все равно к моменту его смерти все величие его открытия в математике и науке вообще не было осознано.
Как многие ученые, Лобачевский попытался доказать постулат Евклида. Он провел через точку пучок прямых, параллельных данной, и стал делать выводы. Делал, делал, противоречие все не появлялось, и в какой-то момент он осознал, что его и нет! Просто если опираться на другой постулат, то появляется другая геометрия! Геометрия Лобачевского очень сильно отличается от евклидовой. Например, сумма углов треугольника может быть какой угодно. Две прямые могут иметь две точки пересечения, и вообще все не так.
Лобачевский к этому времени уже был ректором Казанского университета, параллельно с этим он преподавал и заведовал университетской библиотекой, сам там разбирал книжки и вытирал пыль со стеллажей. Как он все успевал, в принципе непонятно – это невозможно. Он, например, добился того, что в университете были построены новые здания, отвечающие самым современным требованиям. Пока следил за строительством, он вник в архитектурные и экономические тонкости, и в результате денег на строительство было потрачено меньше, чем выделено. Пожалуй, это единственный случай в истории человечества.
Когда в Казани началась эпидемия холеры, оказалось, что он знает, как защититься от заразы. В приказном порядке он переселил на территорию университета всех сотрудников и их семьи. Все они подчинялись строгим правилам карантина. В результате потери от холеры в университете были ничтожно малы по сравнению с городскими, где следовали традиционным методам лечения.
Все это дает представление о том, каким необыкновенным человеком он был. Его авторитет в Казанском университете был абсолютным. Но, когда он выступил с докладом о неевклидовой геометрии, он не был понят. Завистники даже шептались, что он переутомился, ну и... того... ну, бывает. Надо, наверно, менять ректора... но шептались они тихо.
Лобачевский не сдавался, снова и снова с разных точек зрения обосновывал свою теорию, но лишь к концу 19 века научная общественность осознала, что он был абсолютно прав.
Николай Иванович был современником Гаусса, который тоже был признаваем в научном мире и даже носил прозвище короля математиков. После смерти Гаусса в его архивах нашли записи, которые показывали, что он независимо от Лобачевского пришел к подобным результатам. Но опубликовать их он не решился – то ли сам себе не верил, то ли, в отличие от Лобачевского, побоялся уронить свой авторитет.
Был еще один человек, который одновременно с Лобачевским и Гауссом изобрел неевклидову геометрию. Это венгерский математик Януш Бойяи. С ним вообще была трагическая история – пока он доказывал и обосновывал свою теорию, чтобы все было безупречно, Лобачевский успел опубликовать свою. Гаусс отзывался о Бойяи одобрительно, но тот почему-то подозревал Гаусса в том, что он присваивает себе его результаты. А когда вышла статья Лобачевского, Бойяи решил, что это псевдоним, под которым Гаусс публикует украденную у него идею. От этого всего он впал в депрессию, перестал работать и рано умер.
Тем не менее, в истории математики все три имени связаны с созданием неевклидовой геометрии. Все трое пришли к этому каждый своим путем примерно в одно время.
Про точку.
Точка, вообще-то, – это неопределяемое понятие. Но у Евклида очень красиво сказано про точку: «Точка есть то, часть чего есть ничто».
Автор статьи: Тамара Скворцова,
учитель математики (г.Санкт-Петербург).
Фотография Светланы Ершовой.
Опубликовано 7 ноября 2013 г.
Комментарии к статье
Поучительные истории . Записки учителя математики
07.11.2013, 21:31
Елена
Спасибо большое. Обязательно почитаем вместе с сыном.
08.11.2013, 08:11
Валентина
О! Какой интересный материал! С детьми увлекаемся стихосложением, буду использовать для лучшего запоминания
08.11.2013, 13:27
Олег
спасибо очень интересно
26.11.2013, 03:24
Ирина
Большое спасибо Вам за эту подборку!
Очень интересно! Успехов Вам и Вашим ученикам!
29.11.2020, 14:55
Алексей
Спасибо,Тамара.
Очень увлекательный материал и прекрасная подача. Думаю эти статьи должны занять место в книге с названием что-то вроде "О математике и математиках". В вас чувствуется искреннее желание заразить математикой как реальной жизнью,а этого сейчас так не хватает.
|
|
|
Оставить свой комментарий